
接着剤がらみの話になると必ず出てくるのが粘度である。
粘度は液体の流れにくさを表す数値で値が大きいほど流れにくい、つまりドロドロ度を荒らす数字である。
粘度を質量で割ると動粘度という値になる。流れ安さみたいなものを表す。
こちらは言ってみれば体重の割にはサラサラかドロドロかといった事を表す。ドロドロでも軽いものは流れやい、サラサラでも重いものは流れにくいということだ。
粘度というのは液体に生ずる速度勾配とせん断力との比で表されるというか定義される。
理論値と実験値が比較的簡単に一致する例というのはあまりないのだが、比較的細い管の中を圧力で流れる液体の状態は計算と実物が一致する。
ポアジュイユ流れと呼ばれ、定義式を円筒座標に置き換えて積分すると求まる。
半径R、距離Lの液に圧力差Pがかかるときの 中央部を0とした半径rでの速度分布は
U=P/(4μL)*(R^2-r^2)
壁際は0で、中央が最も早い放物線になる
中央の流速は r=0で
Umax=P/(4μL)*(R^2)
流量は
Q=πP/(L8μ)R^4
それでも管を流れる流体の圧力を測るというのは難しい。
自重で縦に流れ落ちる時はどうなるかの式を探したがありそうで無いので、これを参考し自分で導いてみた。
その結果、液体の質量をγとするとうまくLが消えてもっともらしい式が得られた
U=γg/4μ(R^2-r^2)
Umax=γg/4μR^2
Q=γgπ/(8μ)*R^4
これでシリンジに入れて縦に流れ落として重量流量を測れば粘度が求められる。
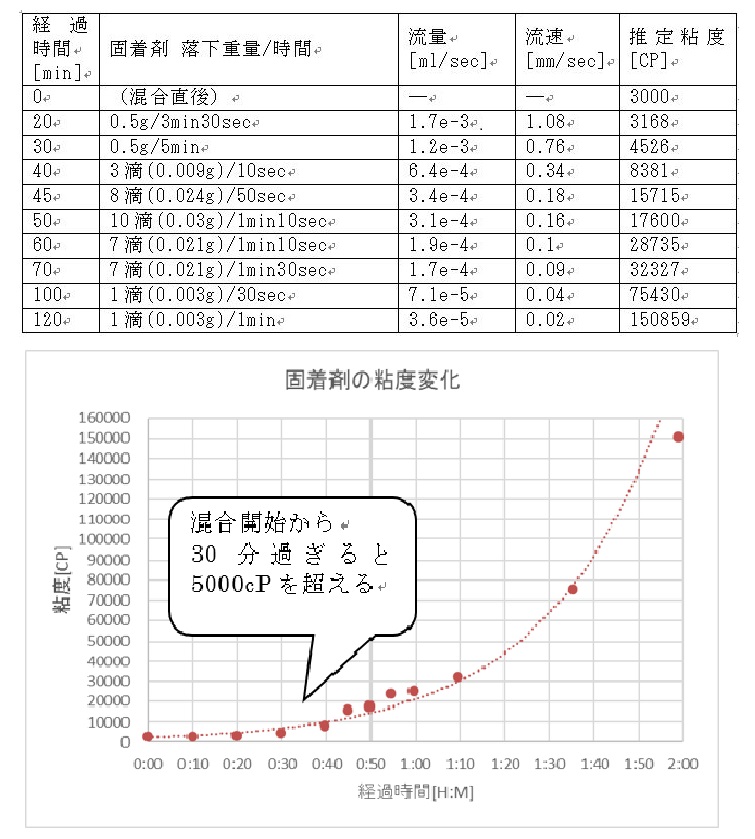
接着剤をシリンジにいれて時間経過と流れ落ちる量を計算したけっかグラフがられた。
攪拌直後からの粘度変化を調べて、5000CP以内で使う方が良いという結論を出したかったのでまあいい結果ではある。
実は流量がちょと違うだけで計算した粘度はかなり変わるのである。流量も粘度が上がってくると測るにも時間がかかるし、いよいよ電子天秤で測れなくなったので滴数を数えている。けっこういい加減な値なのである。
だからわりあい、もっともらしい様に見えるが、かなりいい加減なグラフなのである。内緒だが・・
この項完。
[2018.11.2]
戻る
