
固着剤を使った部品の固定や隙間を埋める作業をポッティングと呼ぶが、たいていの場合気泡が無い事が要求される。
ずいぶん前だがリニアモーターでエアベアリング浮上という製品に携わったことがあるが、その時は駆動用のコイルをポッティング(含浸)表面を研削して平らにし、エアベアリングを作った、エアベアリングの浮上量は10μm程度なので、平面度は5μm以下、削って気泡が出てくると性能の低下やゴミの混入を招くのでNGだった。
今回は防爆の為のポッティングだったが気泡は無き事であった。
どうしても流し込む時に空気の巻き込みは避けがたいが、もともと樹脂の中にある空気は抜きたい、固着剤は2液混合(主剤と硬化剤)の物が多く、混ぜた時にも空気の混入は避けられない。
脱泡法として真空脱泡がある。真空にすることで固着剤の空気を抜く。
最終的にシリンジに詰めて充填したいので、シリンジに充填した後で真空脱泡することにした。
内径φ23、30ml で70mmくらいの長さになる、上向きにして噴き出しても良いようにφ2の出口にチューブをつけて瓶へ逃がすようにし真空容器内で脱泡する。
さて真空脱泡の適切な時間ってどう考えたら良いだろうか。
固着剤の中には2種類の気体が含まれる、混入した空気と液に溶け込んでいる気体だ。
周囲が真空になると混入した泡は大きくなる、ボイルの法則だ、溶け込んでいる気体も出現する。とは言っても真空ポンプで引かれるのは固着剤から抜けた気体で、液から抜け出すのは浮力によることになる。
カレーが煮えて泡が出るような状態である。負圧なので熱をかけなくても泡が出る。
脱泡時間はこの泡が無くなるくらいが目安と言われている。
φ23, 70mm のシリンジで7分くらいが妥当に思われた。
これをなんとか理詰めで証明できないだろうか。
前述したように泡が抜けるのは浮力だから、底に出現した泡が液の表面に上がってくる時間が最低限の脱泡時間ではなかろうか。と、考えた。
終端速度という考え方がある。ストークスの式である。
空気中を落下する球体は空気による浮力と抵抗を受けるがある速度で平衡状態になる、これを終端速度と言い、重力と、浮力と空気抵抗の運動方程式を解くことで導かれる。
これだ!と思った。この場合の空気と物体を逆転させれば、浮力で浮き上がる泡が重力と液体による抵抗を受けることになる。
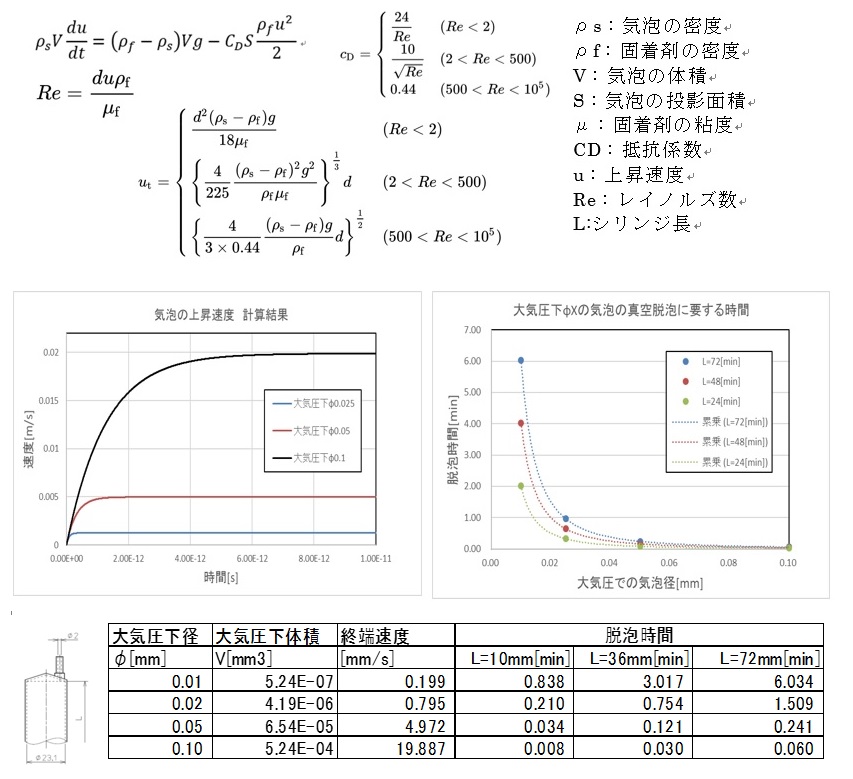
定常状態の解析解も求められているが、レイノルズ数、つまり気泡周りの流れが層流か乱流かによって抵抗部分が異なる、終端速度が判らないとレイノルズ数がわからないので終端速度もわからないと言った循環状態の様だが、仮の速度で仮のレイノルズ数を決めて計算し、矛盾が生じたらやり直すしかない。
終端速度が解れば確かに深さをその値で割れば表面までの移動時間は判る、しかし、終端速度に落ち着くまでの時間が判らないと本当のところは判らない、終端速度になるまえに浮ききってしまうかもしれない。やっぱり非定常の解も必要だがこちらは解析解はとても無理。
そこで差分法で数値解を求めてみた。
一般的に人間の目の分解能は10μmと言われているので、φ0.01の気泡を脱泡できる条件を考えた。その気泡が真空状態で膨らむサイズを求めて終端速度になるまでを追いかけた。
その結果ほとんど瞬間的に終端速度になることが解った。70mmの深さで6分という答えが得られた、すばらしい!!、実験とほぼ一致である。
ではあるのだが、計算に用いた真空度はアルバックの真空ポンプ 到達真空度0.067Pa、大気圧は0.1Mpa=0.1E6Pa であるからなんと 1/1.49e6 気圧である。
この圧力で径0.01mmの気泡が2.9mmになる。
そして固着剤の粘土は5000Cp
装置についてる真空計の読みは 0.001Mpa であるから、本当に真空ポンプの性能いっぱいまで真空になっているかは解らない、粘度も5000CPから上がってしまうと液が硬くなって抵抗も増す。
それでも、粘度の変化を調べたら1時間以内なら5000CPくらいらしいので粘度はまあクリアである。
実験と合っているとはいっても結構厳しい制約である。でも現実にうまくいってるんだからいいよね。
この項完。
[2018.11.4]
戻る
