
機械設計を行うにあたってはネジの締め付けトルクと推力の関係を知りたい場合が結構多い。
特に調整に使いたいネジは推力とトルクの関係に気を使う。
まずは必要な推力を出すネジを手で回せるかどうかの検討、小さいノブで良いのか、蝶ナットが良いのか、ハンドルが必要か、工具で無いと駄目なのか・・といったところ。
特に人が使う治工具はなるべく工具を使わない方が良いので結構重要な選択になる。
また、スクリューネジを使った駆動系の検討に使う事もある。
ネジは斜面の応用だ。荷物を直接真上に引っ張り上げるよりは斜面に沿って引き上げる方が良い。
まずは斜面。摩擦が無い場合、あるいは車輪だと、坂道の傾斜をΘ[°]あるいは[rad]とすると、物体の質量がWの時と、斜面に沿って引く力 F[N]は
F=Wg・sinΘ
物体の質量に限らないよう下方へかかる力と考えQ=Wgとすれば
F=Q・sinΘ
真横に押しても角度が緩ければ斜面を上がっていく
その時の力 Fv は
F = Fv・cosΘ = QsinΘ
Fv = QtanΘ
摩擦があるとちょと複雑になる
物体が斜面を押す力Nは
N=QcosΘ
摩擦係数をμとすると斜面に沿った力に摩擦力が抗力として働く
Fn=Nμ= μQ・cosΘ
斜面に沿った引き上げる力は
F=QsinΘ+μQcosΘ = Q(sinΘ + μcosΘ)
真横に押す力は、その分力が摩擦力を大きくする作用もあるので
F=Fv・cosΘ , N = QcosΘ + Fv・sinΘ
Fv・cosΘ = F + μFv・sinΘ = Q(sinΘ + μcosΘ) + μFv・sinΘ
Fv(cosΘ - μsinΘ) = Q(sinΘ + μcosΘ)
Fv= Q(sinΘ + μcosΘ) /(cosΘ - μsinΘ)
ここで
μ=tanρ=sinρ/cosρ となるρを導入する、ρを摩擦角と呼ぶ
Fv = Q(sinΘ + sinρ/cosρcosΘ)/(cosΘ - sinρ/cosρcosΘ)
=Q(sinΘcosρ + cosΘsinρ)/(coaΘcosρ - cosΘsinρ)
角の和とsin、cos の関係の式から
=Q(sin(Θ+ρ)/cos(Θ+ρ)
Fv = Qgtan(Θ+ρ)
となる。
押し下げる場合を考えると
斜面に沿った引き下げる力は
F+Q・sinΘ=μQ・cosΘ
下げる方向に真横に引けば、その分力は摩擦を減らす作用もあるので、
F=Fv・cosΘ , N = QcosΘ - Fv・sinΘ
Fv・cosΘ + QsinΘ = μ(QcosΘ - FvsinΘ)
Fv(cosΘ + μsinΘ)=Q(μcosΘ - sinΘ)
Fv = Q(μcosΘ - sinΘ)/(μsinΘ + cosΘ)
=Q(sinρ/cosρ・cosΘ - sinΘ)/(sinρ/cosρ・sinΘ + cosΘ)
=Q(sinρcosΘ - cosρsinΘ)/(cosρcosΘ + sinρsinΘ)
=Qsin(ρ-Θ)/cos(ρ-Θ)
Fv=Qtan(ρ-Θ)となる
ρ-Θ < 0 ρ < Θ となるとFvが無くてもQだけで滑り落ちる
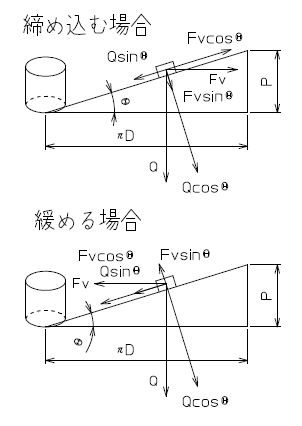
ネジとして考えると、この斜面がぐるっと巻かれている形になる。
横へかかる力Fvはネジを回す力で、ネジの有効径をDとすれば
ネジを回すトルクは
T = Fv・D/2
従ってネジを締めるトルクと推力の関係は
T = Qgtan(Θ+ρ)・D/2
と表される。
一周した時の移動量がネジのリード:Lになるので
傾斜の角度 Θ=atn(L/(πD)
となる。
ところで余談だが、摩擦というのは不思議な力だ。
力がかかる面積には無関係である。
この場合、斜面の絵のままの荷物が落ちる絵をぐるっと巻いて全面接触するネジにしてもμの扱いが変わらないのはこの理由による。
だから溝のあるタイヤもスリックタイヤも摩擦的には変わらない事になる。溝によるひっかかりによって溝のタイヤの方が駆動力があるということか・・
靴底とソリの下面の摩擦係数が同じなら乗っても担いでも滑り方は同じなのかなあ・・
いろいろなサイズのネジについて表にしました。摩擦係数μは0.4としました。結局はこの値によって振られてしまう事になる。
ネジの締め付け力と推力計算エクセルファイルのダウンロード
この項完。
[2019.1.10]
戻る
