
温度と熱の違いは何か。
温度の高いものと低いものを接触させると、高いものから低いものへ熱が移動し、同じ温度になろうとする。熱とは何だろう、物体を構成している分子や原子が振動するということが温度が上がるという事らしい、熱とはエネルギーの一形態であり、温度とは物体を構成している原子や分子の度合いであり、熱を伝えるのは電子が行う。
原子や分子の振動はいくらでも大きくなる、だから高温に限界は無い、でも逆に動きが止まるとそれ以下は無い、動きが止まった時の温度が絶対零度(K=0)、-273℃と呼ばれ、低温には限界があるのだ。
熱が固体内を移動することを熱伝導という。
そして、物体は温度が上がると寸法が大きくなる。これを熱膨張と言い、物質に寄ってその大きさは異なる。その大きくなる状態を制限されると、物体を曲げたりのばしたりした時と同じように物体に力がかかる、これを熱応力といい、物体が曲がったり伸びたり、破壊されたりする。
高温になる装置を考えるときに温度の伝わり方を予測することは大事である。
熱伝導方程式と言うものがある。
熱の伝わり方は物質に寄って異なる。熱の伝わりやすさを熱伝導率λと言う。
言葉で表すと、単位温度勾配、単位面積あたりに伝わる熱量で、[W/mK]の次元を持つ。
伝熱量は[W]=[J/s] 1秒間に1J(ジュール)の熱量が移動した時1W(ワット)の次元を持つ。
電力の[W]と同じで、電圧1V、電流1Aの電気がヒーターに流れている時の発熱量が1[V]×1[A]=1[W]となる。
熱の流れが1方向の時を熱伝導方程式で表そう。
温度勾配 dT/dx(dx[m]の距離でdt[K]の温度差)で伝熱面積がA[m2]、熱伝導率がλ[W/mK]の時に流れる熱量は
q[J/s]=-λA dT/dx と表される。dt時間流れると、熱量は
Q[J]=-λA dT/dx dt
1次元なので、微小部分dxを考えると上流と下流、流れ込みと流れ出しがある。
微小部分dxへ流れ込む熱量は Qin[J]=-λA dT/dx・dt
微小部分dxから流れ出る熱量は Qout[J]=-λA (dT/dx + d(dT/dx)/dx・dx)dt
熱収支は
Qin-Qout=λA(d(dT/dx)/dx・dx)dt = λA(d2T/dx2)dxdt
その微小部分dxにdt時間に流れ込んだ熱量による温度上昇は
体積V=Adx、密度ρ、比熱Cによる、その部分の熱容量VCρで割れば求まるので
dT=(Qin-Qout)/(CρAdx) = λA(d2T/dx2)dxdt/(CρAdx) = λ/(Cρ) d2T/dx2・dt
という2階の微分方程式になる。
dT/dt = λ/(Cρ)d2T/dx2
この微分方程式を解けば解析的に求まることになるが、一般的には数値解が求まれば良いので、差分法を使うと手っ取り早い。
ちなみにλ/(Cρ)を温度伝導率と呼ぶ。
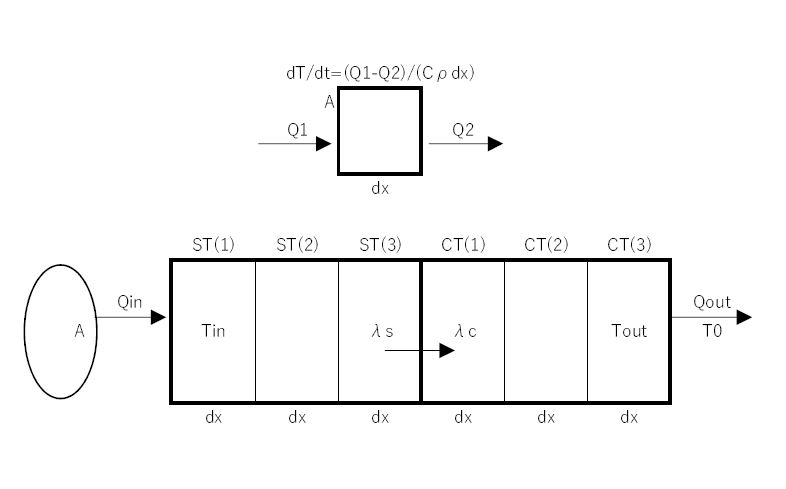
距離dxの三つの要素の温度 T(1), T(2), T(3) を考えて、中央のT(2)の温度上昇を求めよう
T(1)⇒T(2) の熱量 Q1=-λA(T(2)-T(1))/dx・dt
T(2)⇒T(3) の熱量 Q2=-λA(T(3)-T(2))/dx・dt
T(2)へ流れ込む熱量は Q=Q1-Q2=λA(T(1)+T(3)-2T(2))/dx・dt
これを熱容量(AdxCρ)で割ると
dt時間のT(2)の上昇量は
ΔT(2) = λ/(Cρ)(T(1)+T(3)-2T(2))/dx2・dt
と表される代数計算になる。
これがまさに、微分方程式の差分法による代数計算への置き換えになる。
dt時間後のT(2)は計算されたΔT(2)でT(2)+ΔT(2)となる。
この式は個体内の熱伝導を表すが、物体の端部の放熱や、異なる物質間の熱移動は式の形が異なってしまうので、1方向づつの流れを計算して熱収支を考える方が計算しやすいので
ΔT(2) = (Q1-Q2)/(CρAdx)dt
の形で考え、その時々でQ1、Q2をそれぞれ計算した方が式を作りやすい、
このように、ある時刻の状態量からdt時間後の熱収支を求め温度の増減を計算していく。
熱伝導率が異なる物質の境界はどう考えるか、
右図の、二つの物質が組み合わさったモデルを例にとる。
λsとλcの熱伝導率が異なる部分の考え方だ。
ST(3)→CT(1) で、dxの間隔の中央の温度をTとすると
境界の温度をTとすると
ST(3)→T Q1=-λs(T-ST(3)/(dx/2)・dt
T→CT(1) Q2=-λc(CT(1)-T)/(dx/2)・dt
Q=Q1=Q2であると考え
Q=-λ(CT(1)-ST(3))/dx・dt
λ=2λsλc/(λs+λc)
という合成された熱伝導率を得る
放熱の場合はニュートンの冷却の法則を使う事になる。
この場合の熱移動は熱伝達率αを使って
Q=ΔTαA・dt となる。
温度勾配を考慮出来ないのでこうなる。熱伝導と熱伝達の違いである。
ΔTは周囲空気と物体の温度差になる。
熱伝達率αは自然の放熱の場合と、風などを送る強制冷却で異なるので別途求め方を考えねばならないが、実験的に求めた値が伝熱学の本などに載っている。
さて、境界条件の与え方だが、温度で与えてしまうのが考えやすい、ヒーターなどでの過熱の場合は熱流束(流れ込む熱量)で与えるのが現実に即している。
これも解析解では難しいが差分法ならば比較的簡単に実現できる。
右図のφ50ほどのステンレスの棒と銅の棒が繋がっていて、ステンレスの端を過熱、銅の先端から放熱というモデルを作ったので参考にされたい。
dx=10mm という全長60mmの棒である。
ST(1),ST(2),ST(3)がSUS316、CT(1),CT(2),CT(3)が銅で、3分割づつとした。
境界条件としては、温度を与えたモデルとなっている。
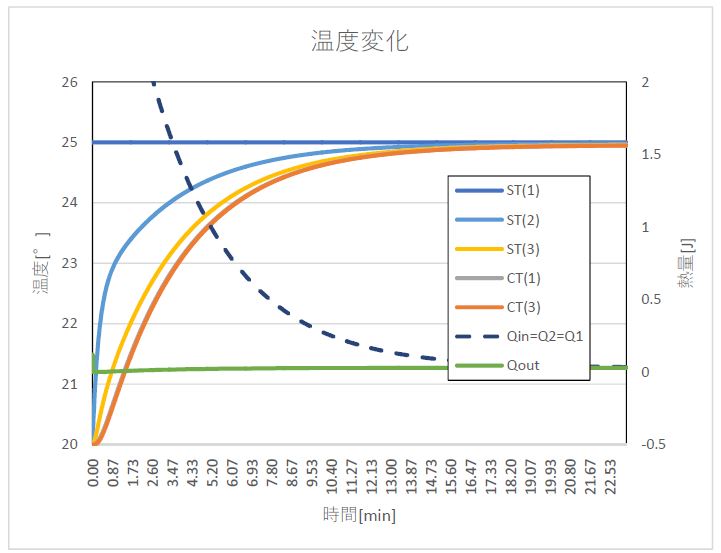
初期は空気の温度で20℃で一様、左端が25℃にステップ状に変化した後の温度変化を計算している。
自然放熱 熱伝達率6[W/m2K]では放熱効果は少ないので全体に25℃に達して定常状態になる。
銅は熱伝導が高いので、銅部分は、ほぼ一様に温度上昇することが判る。SUS316部分は最初は温度差が生じているが、それが徐々に小さくなっていく。
放熱のカーブとST(1)からST(2)への熱移動が一致したところが定常状態ということになる。
差分法の場合はメッシュの大きさや物性値で発散してしまい計算が出来ない場合がある。時間の差分を小さく取るしか方法は無いので、その場合は沢山の計算をしなければならなくなるので、パソコンの性能が上がったからこそ出来る計算法といえる。
ファイルが大きくなってしまうので計算は途中まです。ローカルに続けてください。
1次元熱伝導計算エクセルファイルのダウンロード
差分法は微分方程式を代数的に解く方法なので、他にも応用が効き便利である。微分方程式さえ判っていれば、有限要素法よりも簡単に数値解が求まる。
この項完。
[2019.1.5]
戻る

