
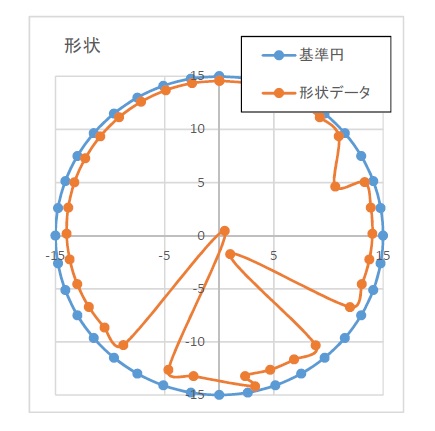
オシロスコープのリサージュデータとか。
顕微鏡で測定した円形データから真円度を求めるとか。
X,Yデータを円にフィッティングしたいということがあるかと思う。
データは、X,Y座標の2次元。円の中心を最小自乗法で求めれば良いのだが・・・
円の方程式は
(X-X0)^2+(Y-Y0)^2=R^2なので、定義から計算してみた。
どうしても、X、Yそれぞれの平均値が中心という結果になってしまう。
データが極めて多い場合はそれで近似できるが、少ない場合は当てはまらない・・・。
原理は判っても自分で式を導くのは案外難しい。
式をうまく変形すると可能になる。
円を表すモデルは
(X(n) - a)^2 + (Y(n) - b)^2 = r^2
なので、これを展開して
X(n)^2 - 2aX(n) + a^2 + Y(n)^2 - 2bY(n) + b^2 - r^2 = 0
整理すると
(X(n)^2 + Y(n)^2) = 2aX(n) + 2bY(n) - (a^2 +b^2 - r^2)
ここで、
c = -(a^2 +b^2 - r^2)
とおけば
(X(n)^2 + Y(n)^2) = a(2X(n)) + b(2Y(n)) + c
という、a,b,cに関する1次方程式になり、これがn=1,2,3....,N (N=測定点の個数)
だけ並んでいる事となる。
これならば、最小自乗法の定義から、円の中心a,b とcが分かり、a,b,cから 半径r が計算できる、結果だけ記すと。
(n)を省略して、行列で表し、
sum((2*X)^2) sum(2X・2Y) sum(2*X)
sum(2X・2Y) sum((2*Y)^2) sum(2*Y)
sum(2*X) sum(2*Y) sum(N)
の行列に
a
b
c
a,b,c を作用させると
sum(2X(X^2+Y^2))
sum(2Y(X^2+Y^2))
sum(X^2+Y^2)
となる。
逆行列を求めれば、 a,b,c が算出できる。
最小二乗法によるデータ群の円へのフィッティングのダウンロード
基本的な関係式が解っていれば係数の推定ができるので使えると便利なアイテムです。
この項完。
[2019.2.20]
戻る
